介绍:
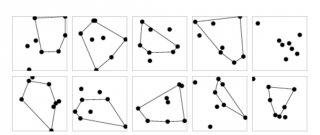
(此前一次录音质量太差,故重录,因此称为“修复版”)本节目开通了微信公众号,欢迎订阅:[图片]请你在一张纸上随便画5个点,里面不要有三点共线的情况,其他都随便画,然后请你尝试在这5个点里随便找4个点连接起来,唯一要求是构成一个凸四边形。然后你很快会发现,是不是随便画5个点,都能找出这样的四个点来构成凸四边形。但是很显然,只有四个点的话,不一定能构成凸四边形。那我现在问你,你能否证明构成凸四边形是否至少就需要5个点呢?如果要构成凸五边形,那至少需要多少个点呢?如要凸11边型又如何呢?这个一般的,平面上至少需要多少个点来构成凸n边型的问题,就是所谓幸福结局问题。1933年,厄多斯和塞凯赖什证明了g(n)的上下界:[图片]2016年,有人证明:[图片]凸5边型的情况和一个反例:
大家还在听

