介绍:
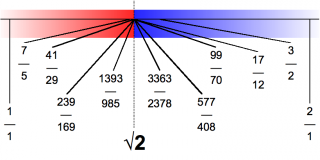
“为什么说实数是连续的，能够布满一条数轴？” 相对应的，为什么有理数就不行，也就是有理数是不连续的，有很多断点的？.....前面戴德金拉拉杂杂说了那么多，现在重点来了，他其实就是想说，既然分割点不一定是有理数，那我就定义一种数叫“实数”，每个实数就对应以上的一种对“有理数”的切割，也就是一对左集和右集，唯一对应一个叫实数的数。这个定义重要的一点是，它是根据有理数定义出来的，而没有用到更多前提；第二点，根据切割的定义，我们可以知道切割出来的实数天然具有有序和稠密性，而且它的定义就证明它与直线上的点是对应的，因为实数就是对直线任意位置切割产生的，所以它就是与数轴对应的！而这种“连续”，也被称为“戴德金完备”性，也就是说完整了。戴德金切割图示：[图片]订阅“大老李聊数学”公众号[图片]
大家还在听
