28. 神秘的0.577--欧拉-马斯刻若尼常数

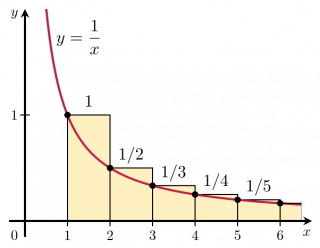
很有趣，略带神秘感。要知道这个常数的来由，我们可以先从一个小故事开始。有一只蚂蚁，在一根橡皮绳上的一端，橡皮绳初始长度为1m，然后蚂蚁开始爬，它的爬行速度是每秒1cm，但橡皮绳每1秒后，又会均匀拉伸1m长，也就是1秒后，绳子变2米，再一秒后，变3米长，等等。问你这只蚂蚁能否爬到橡皮绳的另一端？[图片]上图中，黄色部分位于1/x曲线以上的部分面积之和，即为欧拉-马斯刻若尼常数。每周一题：阴影部分面积多大？ （附上周答案）本周题目：阴影部分面积多大？如下图，有一个半径为2的小圆，沿半径为10的大圆逆时针运动，移动半个圆周后，沿一个半径为5的圆继续运动半个圆周。运动过程中，橙色圆圆心始终保持在其他圆上。为橙色圆扫过的面积多大，即图右阴影部分（包含橙色圆本身）？提示：无需高等数学，耐心将图形分解，分部计算。[图片] 上期答案：上周题目是：冯诺依曼曾经出过这么一道有趣的题目：你有一枚不均匀的硬币，它掷出去正反面向上的概率不等，你也不知道具体哪面向上的概率高，概率是多少。请问，你能否用这枚硬币产生50%的概率事件？或者说，你可以用这枚硬币公平的与别人打赌？要求：只能用投掷硬币的动作，只有一枚这样的硬币，不能使用其他工具。提示：可以投掷不止一次，别想太复杂。很多读者想出了这样的办法：两人轮流掷，看谁先掷出最多的正面或背面，类似于足球比赛的罚点球。此方法可以，但太过复杂。冯诺依曼给出的方法是：你可以这样打赌说：我们分别选择“正反”或“反正”，连掷两次这枚硬币，看先出现“正反”还是“反正”，先出现为胜者。如果结果是“正正”或“反反”则重掷。以上方法不但简单明了，而且操作性也很强啊！下周再见！收听“大老李聊数学”音频                                        关注“大老李聊数学”[图片] [图片]