(文末有每周一题和上周答案)

今天跟大家聊一个近期的数学新闻。这个新闻是关于这样一个问题：什么样形状的地砖可以铺满地板不留缝隙？你可能马上能想到正三角形，正方形和正六边形都可以。那如果不是正多边形的呢？这个问题一下子有意思起来，这就牵涉到数学中所谓的密铺问题。密是密密麻麻的的密，铺是铺地板的铺。

任意三角形密铺：

任意四边形密铺：

六边形密铺：

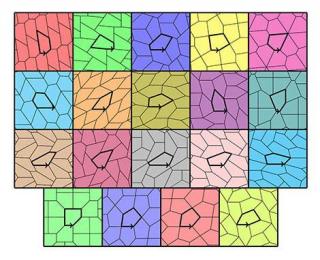
15种五边形密铺(含4中特例)：

非周期性密铺--彭罗斯镶嵌：

---

每周一题 本周题目：能变成一样颜色吗？

本期题目取自俄罗斯某数学竞赛题。某岛屿上有一群变色龙。现在有13只绿色的，15只蓝色的和17只红色变色龙。每当两只不同颜色的变色龙靠近时，它们都会变成第三种颜色。那么它们有可能变成同一种颜色吗？

---

上期答案：

上周题目是：

如下图，有一个半径为2的小圆，沿半径为10的大圆逆时针运动，移动半个圆周后，沿一个半径为5的圆继续运动半个圆周。运动过程中，橙色圆圆心始终保持在其他圆上。为橙色圆扫过的面积多大，即图右阴影部分（包含橙色圆本身）？

提示：无需高等数学，耐心将图形分解，分部计算。

这期题目比较简单，答案是64pi。答对的朋友有(如有遗漏请见谅)：黄亮，今年不买表，李凯峰_3g，Matody 。

解法看这个图就明白了：

另外还有两位朋友(567和吃喵个鱼)提出这种解法：大圆半周长＋小圆半周长，然后乘以小球半径，然后再加上小球的面积。你看，微积分思想就是这样孕育出来的。下周再见！

收听“大老李聊数学”音频                                        关注“大老李聊数学”